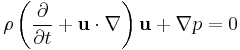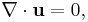Inviscid flow

In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow.[1]

The flow of fluids with low values of viscosity agree closely with inviscid flow everywhere except close to the fluid boundary where the boundary layer plays a significant role.[2]

Contents

Reynolds number

The assumption of inviscid flow is generally valid where viscous forces are small in comparison to inertial forces. Such flow situations can be identified as flows with a Reynolds number much greater than one. The assumption that viscous forces are negligible can be used to simplify the Navier-Stokes solution to the Euler equations.

In the case of incompressible flow, the Euler equations governing inviscid flow are:

\rho\left( \frac{\partial}{\partial t}%2B{\bold u}\cdot\nabla \right){\bold u}%2B\nabla p=0
\nabla \cdot \mathbf{u} = 0,

which, in the steady-state case, can be solved using potential flow theory. More generally, Bernoulli's principle can be used to analyse certain time-dependent compressible and incompressible flows.

Problems with the inviscid-flow model

While throughout much of a flow-field the effect of viscosity may be very small, a number of factors make the assumption of negligible viscosity invalid in many cases. Viscosity cannot be neglected near fluid boundaries because of the presence of a boundary layer, which enhances the effect of even a small amount of viscosity. Turbulence is also observed in some high-Reynolds-number flows, and is a process through which energy is transferred to increasingly small scales of motion until it is dissipated by viscosity.

References

Notes

  1. ^ Clancy, L.J., Aerodynamics, p.xviii
  2. ^ Kundu, P.K., Cohen, I.M., & Hu, H.H., Fluid Mechanics, Chapter 10, sub-chapter 1

See also